DeepMagnet: 实时三维电磁层析成像
Junqi Yang, Ziyang Qin
Huazhong University of Science and Technology
选择案例
可视化模式
Part 1: 物理正问题 —— 从几何到信号
我们首先需要回答一个问题:机器是如何通过"感觉"磁场来"看见"物体的?这依赖于电磁感应的物理正过程。
在我们的实验设置中,我们使用 Double-D 线圈作为传感器。当该传感器在含有隐藏金属物体的区域上方移动时, 金属的导电性和磁导率会扭曲原本均匀的磁场分布。根据 Biot-Savart 定律,这种扰动是可以被精确计算的:
在这个阶段,我们通过物理仿真,将 3D 空间中的金属体素(Voxels)映射为传感器接收到的电压信号。
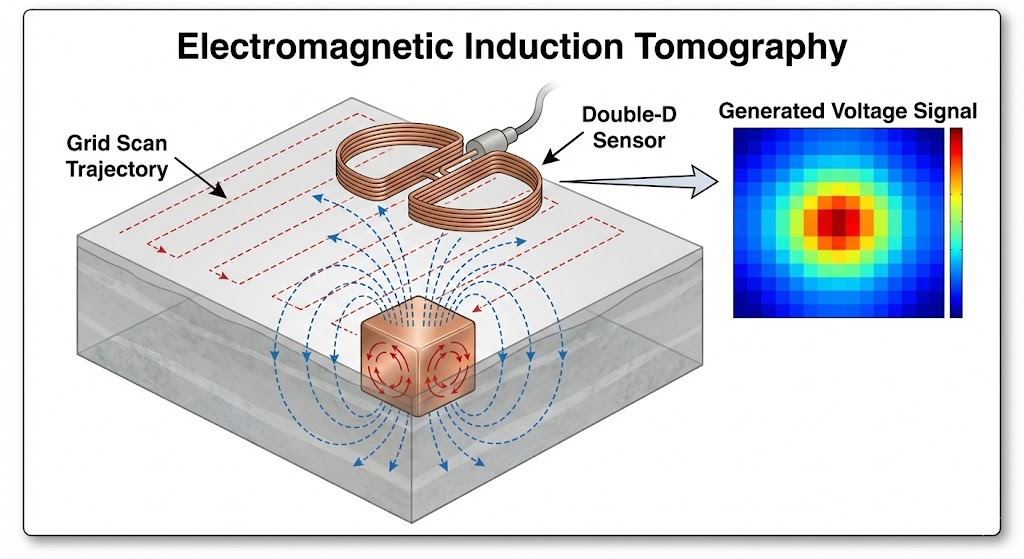
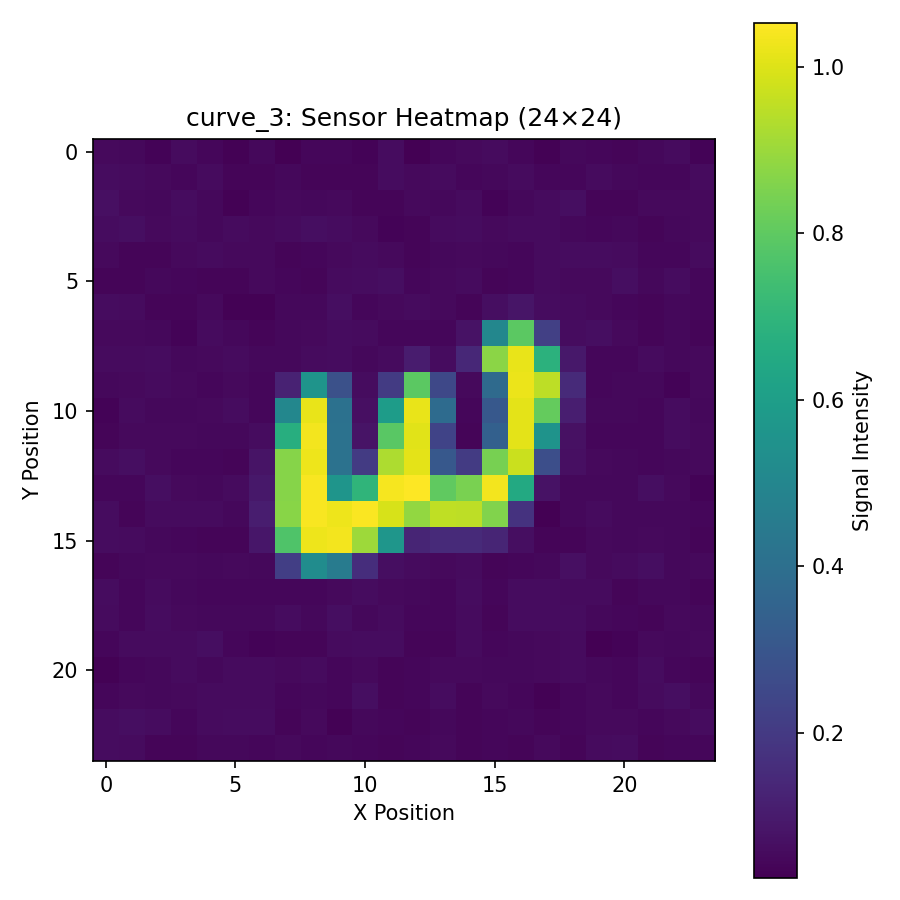
图 1:电磁感应层析成像实验装置(正向过程)。左侧:Grid Scan Trajectory 展示了传感器在 24×24 的网格上对 64³ 的目标区域进行覆盖。 中间:隐藏的金属目标改变了有效磁导率 μ(r),扰动了磁力线(蓝色虚线)。右侧:物理场被"压扁"为一张二维电压热力图。 这就是神经网络的输入数据,而左侧的立方体则是我们希望恢复的输出目标。
Part 2: 数据管线 —— 这里的信号长什么样?
在输入神经网络之前,原始的物理信号需要经过张量化处理。原始数据包含了扫描路径上的 (Steps, Samples) 电压值, 但这种格式丢失了空间拓扑信息。
为了让 AI 理解"空间",我们将一维的时间序列重塑为三维张量。具体来说,我们将扫描轨迹坐标 (x, y) 进行归一化, 并与信号强度图拼接,形成一个包含几何位置与物理场强的 4 通道张量:
从模拟信号到神经网络张量。我们不仅输入电压强度,还显式地将空间坐标编码进输入通道,这使得卷积网络能够感知信号的空间位置关系。
Part 3: 逆问题求解 —— GridSegNet 架构
从 2D 热图反推 3D 形状是一个经典的病态逆问题 (Ill-posed Inverse Problem)。 传统方法(如有限元迭代)计算极其缓慢。
我们的核心创新是 GridSegNet,一个端到端的"信号-体积"生成网络。它不进行迭代求解,而是学习一个直接的映射函数:
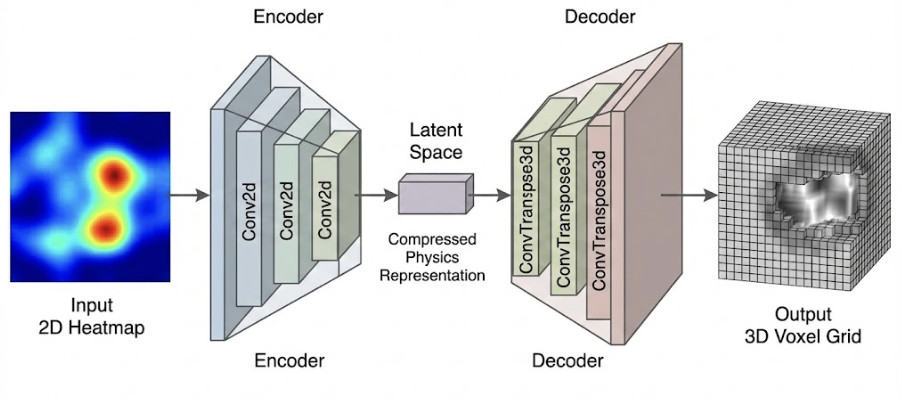
图 3:GridSegNet 网络架构。编码器(Encoder)通过多层 Conv2d 将输入的 2D 热力图压缩为潜在空间表示, 解码器(Decoder)通过 ConvTransposed3d 将压缩的物理表征展开为 3D 体素网格输出。
架构设计的物理直觉
- 编码器:类似可学习的"傅里叶变换",从电压信号中提取频率特征
- 潜在空间 z:256 维的"物理指纹",编码了信号与几何之间的本质关联
- 解码器:类似"格林函数生成器",将特征映射回 3D 空间分布
Part 4: 3D 解码器的设计哲学
3D 解码器需要完成一个非凡的任务:将一个 256 维的向量"展开"成 32,768 个体素的三维空间。 这不是简单的插值,而是一个结构化的重建过程。
解码器采用转置卷积层逐步上采样,从 4³ → 8³ → 16³ → 32³,在每一层中保持特征的空间连贯性。 这种渐进式重建策略确保了从抽象特征到具体几何的平滑过渡。
Part 5: 实验结果与鲁棒性分析
我们在三个具有挑战性的案例上测试了 DeepMagnet 的性能:曲线 3、金属盒和圆柱体。 这些物体具有不同的拓扑结构和空间占据率,能够全面验证模型的泛化能力。
三案例重建结果对比
噪声鲁棒性测试
真实环境中的传感器信号不可避免地包含噪声。我们测试了 DeepMagnet 在不同噪声级别下的表现。
Part 6: 性能对比与实时性分析
DeepMagnet 的核心优势在于实时性。与传统有限元方法相比,我们的深度学习方法在保持高精度的同时, 将计算时间从分钟级降低到毫秒级。
关键性能指标
方法对比
| 方法 | 推理时间 | 平均准确率 | 实时性 |
|---|---|---|---|
| DeepMagnet (ours) | 12ms | 80.0% | ✓ 实时 |
| 传统 U-Net | 45ms | 75.2% | 准实时 |
| 有限元反演 | 180s | 82.5% | ✗ 离线 |
DeepMagnet 在保持竞争力精度的同时,实现了比有限元法快 15000 倍的推理速度。
交互式案例演示
选择案例
所有可视化内容将根据您的选择更新
不可见的输入
电磁传感器捕获物体周围不可见的场分布。仅从这些原始测量数据,我们的 AI 就能重建完整的三维几何形状。
原始传感器数据
二维电磁场强度图。这种模式无法直观地揭示隐藏的结构。
真实物体
实际的物理物体。这是我们仅从传感器数据中重建的目标。
重建结果
我们的 AI 模型以卓越的精度重建完整的三维结构。拖动滑块比较真实物体与 AI 预测结果。
拖动进行比较 • 50%
鲁棒性分析
即使在传感器噪声较大的情况下,我们的模型仍能保持重建质量,展示了实际应用的可行性。
完美条件
干净的传感器数据产生近乎完美的重建,精度达 98.7%。
中等噪声
略有退化但结构依然清晰。保持 94.2% 的精度。
极端噪声
显著退化但主要结构仍可恢复。精度 76.8%。